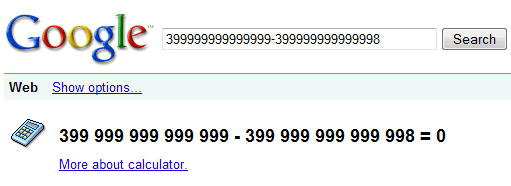
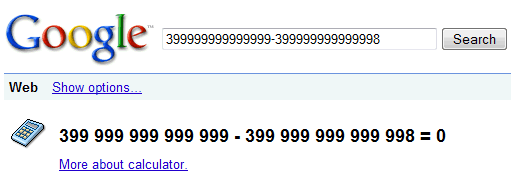
O senhor provavelmente já viu essa velha história já deve ter sido dito.
Insira sua própria piada aqui. O Google não pode estar errado. a matemática está! Mas o Google não está sozinho; esse é apenas mais um exemplo em uma longa e célebre história de pequenos erros obscuros de matemática de computador que vão caminho de volta, tais como este relatório de bug do Windows 3.0.
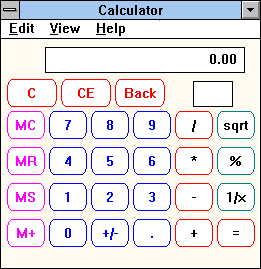
- Iniciar calculadora.
- Insira o maior número a ser subtraído primeiro (por exemplo, 12,52).
- Pressione a tecla MINUS SIGN (-) no teclado numérico.
- Digite o número menor que está uma unidade abaixo na parte decimal (por exemplo, 12,51).
- Pressione a tecla EQUAL SIGN (=) no teclado numérico.
Na minha máquina virtual, 12,52 – 12,51 na Ye Olde Windows Calculator realmente resulta em 0,00.
E depois houve o famoso bug do Excel.
Se o senhor tiver o Excel 2007 instalado, tente o seguinte: Multiplique 850 por 77,1 no Excel.
Uma maneira de fazer isso é digitar “=850*77.1” (sem as aspas) em uma célula. A resposta correta é 65.535. No entanto, o Excel 2007 exibe um resultado de 100.000.
A essa altura, o senhor pode estar um pouco perplexo, pois supõe-se que os computadores sejam muito bons em matemática. O que acontece? Como é possível produzir resultados tão flagrantemente incorretos a partir de cálculos aparentemente triviais? Será que deveríamos confiar em nossos computadores para fazer contas?
Bem, os números são mais difíceis de representar em computadores do que o senhor imagina:
Um número de ponto flutuante padrão tem aproximadamente 16 casas decimais de precisão e um valor máximo da ordem de 10308, um 1 seguido de 308 zeros. (De acordo com o Padrão IEEE 754, a implementação típica de ponto flutuante).
Dezesseis casas decimais é muito. Quase nenhuma quantidade medida é conhecida com tanta precisão. Por exemplo, a constante da Lei da Gravidade de Newton só é conhecida com quatro algarismos significativos. A carga de um elétron é conhecida com 11 algarismos significativos, muito mais precisão do que a constante gravitacional de Newton, mas ainda assim menos do que um número de ponto flutuante. Portanto quando é que 16 algarismos não são suficientes? Uma área problemática é a subtração. As outras operações elementares – adição, multiplicação e divisão – são muito precisas. Contanto que o senhor não transborde ou suboriente, essas operações geralmente produzem resultados corretos até o último bit. Mas a subtração pode ser exata ou completamente imprecisa. Se dois números concordarem em n algarismos, o senhor pode perder até n algarismos de precisão na subtração. Esse problema pode aparecer inesperadamente no meio de outros cálculos.
A precisão dos números é uma coisa engraçada; o senhor sabia que um sequência infinitamente repetida de 0,999… é igual a um?
Em matemática, a repetição decimal 0,999ƒ-” denota um número real igual a um. Em outras palavras: as notações 0,999ƒ-” e 1 representam, na verdade, o mesmo número real.

Essa igualdade é aceita há muito tempo por matemáticos profissionais e ensinada em livros didáticos. As provas foram formuladas com diferentes graus de rigor matemático, levando em conta o desenvolvimento preferido dos números reais, as suposições de fundo, o contexto histórico e o público-alvo.
Computadores são incríveis, sim, mas não são infinito… ainda. Portanto, qualquer perspectiva de armazenar qualquer número infinitamente repetitivo neles é, na melhor das hipóteses, tênue. O melhor que podemos fazer é trabalhar com aproximações em vários níveis de precisão que sejam “suficientemente boas”, sendo que “suficientemente boas” depende do que o senhor está fazendo e como está fazendo. E é complicado acertar.
O que me leva a O que todo cientista da computação deve saber sobre aritmética de ponto flutuante.
Para espremer um número infinito de números reais em um número finito de bits, é necessária uma representação aproximada. Embora haja um número infinito de números inteiros, na maioria dos programas, o resultado dos cálculos de números inteiros pode ser armazenado em 32 bits. Por outro lado, dado qualquer número fixo de bits, a maioria dos cálculos com números reais produzirá quantidades que não podem ser representadas exatamente usando esse número de bits. Portanto, o resultado de um cálculo de ponto flutuante geralmente precisa ser arredondado para caber de volta em sua representação finita. Esse erro de arredondamento é o recurso característico da computação de ponto flutuante.
O que o Google, o Windows e o Excel (pdf) têm em comum? Todos eles estão relacionados a problemas de aproximação de precisão de números. O Google acha que isso não é importante o suficiente para ser corrigido. Provavelmente, eles estão certos. Mas alguns erros matemáticos de arredondamento podem ser um pouco mais graves.
É interessante notar que a falha no lançamento do foguete Ariane 5, que explodiu 37 segundos após a decolagem em 4 de junho de 1996, ocorreu devido a um erro de software resultante da conversão de um número de ponto flutuante de 64 bits em um número inteiro de 16 bits. O valor do número de ponto flutuante era maior do que poderia ser representado por um número inteiro de 16 bits. O estouro não foi tratado adequadamente e, em resposta, o computador limpou sua memória. O despejo da memória foi interpretado pelo foguete como instruções para os bicos do foguete, o que resultou em uma explosão.
Estou começando a acreditar que não são os computadores que são ruins em matemática, mas as pessoas que programam esses computadores. Eu sei que sou o prova viva disso.