Uma das minhas entradas de blog favoritas de todos os tempos é uma história verdadeiramente épica de namoro que deu errado e que culmina com a mais estranha referência a P=NP que o senhor provavelmente encontrará.
Joey: Então o senhor realmente se formou em engenharia da computação?
Garota nova: Sim, eu fiz, da UBC!
Joey: E o senhor fez o curso “Algoritmos”?
Garota nova: Claro que sim!
Joey: E o senhor tem todos os artigos que escreveu?
Garota nova: Sim! Guardei todos eles e vou mostrá-los aos senhores amanhã!
Joey: Quero ver aquele que sempre chamamos de “Hell Paper” na Queen’s – o trabalho obrigatório do quarto ano. O senhor conhece aquele em que provamos que P = NP?
Menina nova: Eu fiz isso! Provei que P = NP! Fiquei entre os primeiros da turma, e o professor usou meu trabalho como exemplo!
Joey: O senhor provou que P = NP?
A senhora: Sim!
Joey: Entendi.
Pobre Joey. Sair com pessoas loucas é uma coisa, mas sair com pessoas loucas que afirmam ter provado P=NP é outra questão completamente diferente. Eu sei, eu sei, meu histórico com P=NP não é muito melhor. Mas pelo menos o senhor não está namorando comigo, certo?
A completude de NP é um dos grandes mistérios não resolvidos da ciência da computaçãoTalvez a melhor maneira de ilustrar seja por meio do este desenho animado do xkcd:
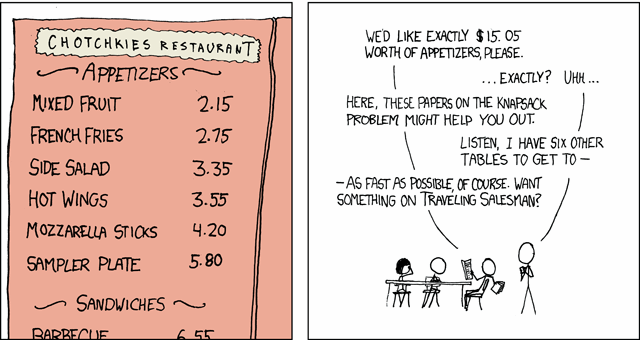
A característica que define um problema NP-completo é que as soluções ideais, usando a matemática e a lógica como as entendemos atualmente, são efetivamente impossíveis. Claro, o senhor pode aproximar uma solução, mas um ideal requer tantos cálculos que se torna inviável, mesmo com computadores que operam, digamos… na velocidade da luz.
Na verdade, um dos problemas mais importantes da ciência da computação é determinar se existem questões cuja resposta pode ser verificada rapidamente, mas que exigem um tempo impossivelmente longo para serem resolvidas por qualquer procedimento direto. Problemas como o listado acima certamente parecem ser desse tipo, mas até agora ninguém conseguiu provar que algum deles é realmente tão difícil quanto parece, ou seja, que realmente não existe uma maneira viável de gerar uma resposta com a ajuda de um computador.
É duvidoso se alguém conseguirá provar que P=NP (pdf), mas, enquanto isso, é útil para o reconhecer problemas que são NP completos:
Infelizmente, provar a intratabilidade inerente pode ser tão difícil quanto encontrar algoritmos eficientes.
A teoria da NP-completude fornece muitas técnicas simples para provar que um determinado problema é “tão difícil” quanto um grande número de outros problemas que são amplamente reconhecidos como difíceis e que vêm confundindo os especialistas há anos. Munido dessas técnicas, o senhor poderá provar que o problema do bandersnatch é NP-completo, entrar na sala do seu chefe e anunciar:

Não consigo encontrar um algoritmo eficiente, mas todas essas pessoas famosas também não conseguem.
No mínimo, isso informaria ao seu chefe que não seria bom demiti-lo e contratar outro especialista em algoritmos.
Agora o senhor pode dedicar seu tempo à procura de algoritmos eficientes que resolvam vários casos especiais do problema geral. O senhor pode procurar algoritmos que, embora não tenham a garantia de serem executados rapidamente, pareçam ter essa probabilidade na maior parte do tempo. Ou o senhor pode até relaxar um pouco o problema, procurando um algoritmo rápido que simplesmente encontre projetos que atendam à maioria das especificações dos componentes. Assim, a principal aplicação da teoria da NP-completude é ajudar os projetistas de algoritmos a direcionar seus esforços de solução de problemas para as abordagens que têm maior probabilidade de levar a algoritmos úteis.
Como acontece com muitas coisas na programação, o primeiro passo é aprender o suficiente para saber quando o senhor está realmente ferrado.
Infelizmente para o pobre Joey, esse triste corolário da NP-completude aparentemente também se aplica ao namoro.