Digamos que o senhor esteja prestes a implementar um aplicativo. Esse aplicativo foi amplamente testado pela sua equipe de desenvolvimento, que foi infectada pela febre dos testes unitários. Ele também foi examinado pelo seu grupo de controle de qualidade, que passou meses vasculhando cada fenda do aplicativo. O senhor até teve um período de teste beta com usuários reaisque, obedientemente, registraram bugs e testaram o aplicativo antes de finalmente aprová-lo.
Seu aplicativo é útil e popular. Seus usuários o adoram. Seus usuários adoram o senhor. Mas, na semana seguinte, algo curioso acontece. À medida que as pessoas usam o aplicativo, ele fica cada vez mais lento. Logo, as reclamações começam a chegar. Em poucas semanas, o aplicativo está quase inutilizável devido a todos os atrasos insuportáveis a que submete os usuários – e seus usuários se voltam contra o senhor.
Levante a mão se isso já aconteceu em algum projeto em que o senhor trabalhou. Se eu ganhasse um dólar por cada vez que vi isso pessoalmente, teria o suficiente para um bom almoço. Os desenvolvedores testam com pequenos conjuntos de dados de brinquedo, presumem que tudo está bem e depois descobrem da maneira mais difícil que tudo é rápido para n pequeno.
Lembro-me de uma rotina de classificação em Javascript no lado do cliente que implementamos em um aplicativo da Web de intranet avançada por volta de 2002. Ela funcionou muito bem em nossos pequenos conjuntos de dados de teste, mas quando a implementamos na produção, ficamos surpresos ao descobrir que a classificação de uma mísera centena de itens poderia levar mais de 5 segundos na máquina desktop de um usuário. O JavaScript não é conhecido por sua velocidade, mas que diabos?
Bem, adivinhe qual algoritmo de classificação que usamos?
O InsertSort é n2 (pior caso), o ShellSort é n3/2e o QuickSort é n log n. Mas nós poderia ter feito pior – poderíamos ter escolhido o Bubble Sort, que é n2 mesmo no melhor caso.
Amigos, não façam isso. Teste seus aplicativos com grandes conjuntos de dados, pelo menos grandes o suficiente para cobrir suas projeções de uso mais otimistas para o próximo ano. Caso contrário, o senhor poderá se arrepender. E seus usuários certamente irão se arrepender.
A notação Big O é uma daquelas coisas que é mais fácil de ver do que de explicar. Mas é um bloco de construção fundamental da ciência da computação.
Notação Big O: Uma medida teórica da execução de um algoritmoO algoritmo é uma medida de tempo, geralmente o tempo ou a memória necessária, dado o tamanho do problema n, que geralmente é o número de itens. Informalmente, dizer que alguma equação f(n) = O(g(n)) significa que ela é menor do que algum múltiplo constante de g(n). A notação é a seguinte: “f de n é grande oh de g de n”.
Os desenvolvedores contam com estruturas de dados e bancos de dados que têm um desempenho favorável da notação big O incorporado, sem pensar muito sobre isso. Mas se o senhor se desviar desses caminhos bem usados, o senhor pode se deparar com um mundo de problemas de desempenho – e muito mais cedo do que poderia imaginar. A importância da notação big O é melhor ilustrada neste gráfico do Pérolas de programação:
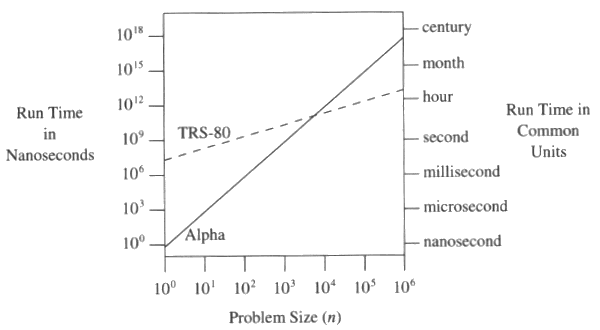
O TRS-80 algoritmo é 48ne o DEC Alpha O algoritmo é n3.
Quando n é 10, eles estão a um segundo um do outro. Mas quando n aumenta para 100.000, o DEC Alpha moderno leva um mês para fazer o que um TRS-80 pré-histórico pode fazer em algumas horas. Ter um grande gargalo de notação O em seu aplicativo é uma passagem só de ida na máquina de retrocesso de desempenho para 1997 – ou pior. Muito pior.
Existem nomes amigáveis para as notações comuns de big O; dizer “n ao quadrado” é equivalente a dizer “quadrático”:
Tom Niemann tem gráficos úteis que comparam as taxas de crescimento de algoritmos comuns, que eu adaptei aqui:
| n | lg n | n7/6 | n lg n | n2 | 7/6n | n! |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 16 | 4 | 25 | 64 | 256 | 12 | 20,9 trilhões |
| 256 | 8 | 645 | 2,048 | 65,536 | 137 quatrilhões | – |
| 4,096 | 12 | 16,384 | 49,152 | 16,777,216 | – | – |
| 65,536 | 16 | 416,128 | 1,048,565 | 4,294,967,296 | – | – |
| 1,048,476 | 20 | 10,567,808 | 20,969,520 | 1,09 trilhão | – | – |
| 16,775,616 | 24 | 268,405,589 | 402,614,784 | 281,4 trilhões | – | – |
Aqui estão exemplos de tempos de execução, supondo que uma unidade de execução seja igual a um milissegundo de tempo de CPU. Isso provavelmente é um exagero nas CPUs atuais, mas o senhor entendeu a ideia:
| n | lg n | n7/6 | n lg n | n2 | 7/6n | n! |
| 1 | <1 seg | <1 seg | <1 seg | <1 seg | <1 seg | <1 seg |
| 16 | <1 seg | <1 seg | <1 seg | <1 seg | <1 seg | 663 anos |
| 256 | <1 seg | <1 seg | 2 segundos | 65 segundos | 4,3 milhões de anos | – |
| 4,096 | <1 seg | 16 seg | 49 seg | 4,6 horas | – | – |
| 65,536 | <1 seg | 7 min | 17 min | 50 dias | – | – |
| 1,048,476 | <1 seg | 3 horas | 6 horas | 35 anos | – | – |
| 16,775,616 | <1 seg | 3 dias | 4,6 dias | 8.923 anos | – | – |
Observe a rapidez com que temos problemas à medida que o número de itens (n) aumenta. A menos que o senhor tenha escolhido estruturas de dados que ofereçam desempenho ideal quase logarítmico em todas as áreas, quando chegar a 4.096 itens, estará falando de grave tempo de CPU. Além disso, usei o como abreviação de “forever” (para sempre). É assim que as coisas podem ficar ruins.
Tudo é rápido para as pequenas empresas. Não caia nessa armadilha. É um erro bastante fácil de cometer. Os aplicativos modernos são incrivelmente complexos, com dezenas de dependências. Se o senhor deixar de indexar um pequeno campo no banco de dados, de repente estará de volta à terra do TRS-80. A única maneira de saber realmente se o senhor inseriu acidentalmente um gargalo algorítmico big O em algum lugar do seu aplicativo é testá-lo com um volume razoavelmente grande de dados.

